Solution – Problem # 1
Twenty-one girls and twenty-one boys took part in a mathematical contest.
(i) Each contestant solved at most six problems.
(ii) For each girl and each boy, at least one problem was solved by both of them.
Prove that there was a problem that was solved by at least three girls and at least
three boys.
For each girl and each boy, at least one problem was solved by both of them. It would be convenient to talk of the problem solved by a particular girl and boy, but there may be more than one. To get round this difficulty, for each pair of boy and girl, we select one of the problems which they both solved, and call it their special problem. Notice, by the way, that we have to do this for all $21 \times 21 = 441$ pairs of kids of different gender.
We say that a problem is male if it is solved by at most two girls (so it is hard for girls), and that a problem is female if it is solved by at most two boys (so it is hard for boys). If we can show that not every problem is male or female, then that problem is solved by at least three girls and at least three boys, and so we will have finished.
We now proceed by contradiction. We assume (hoping to obtain an absurd conclusion) that every problem is male or female (or possibly both). We now look at each of the 441 boy, girl pairs in turn. For a given pair, if their special problem is female, we associate the letter $F$ to this pair. If it is not female, then this problem must be male but not female, and we associate the letter $M$ to this pair of children.
Each one of the 441 pairs is now associated to a letter $M$ or a letter $F$. There are an odd number of pairs, and so one of the two letters must be in the majority. Suppose that it is M. If that is wrong, the argument will be exactly the same, exchanging girls with boys and $M$s with $F$s. We can say “without loss of generality, the letter M is in the majority” because it doesn’t matter which letter is in the majority, the argument will proceed unhindered, by swapping sexes.
Anyway, it is now safe to assume that there are at least 221 occurrences of the letter $M$. Now there are 21 boys, and we look at how many times each boy is involved in a pair associated to the letter $M$, it follows that at least one boy is involved in 11 or more pairs associated to $M$, because if each boy is involved in 10 or fewer pairs associated to M, then there would be at most $21 \times 10 = 210$ occurrences of the letter $M$.
Now focus on such a boy, who is involved in 11 or more pairs associated to the letter $M$. These special problems associated with the letter M are each solved by at most two girls, so this boy has done at least 6 male problems, because if he had done 5 or fewer male problems, then there would be at most $10 = 2 \times 5$ girls with whom, when paired with this boy, could be associated with the letter $M$. However, condition (i) of the problem tells us that this boy has solved at most 6 problems. Therefore this boy has solved exactly 6 problems, and each one of them has been solved by at most two girls. Now look at condition (ii). This condition is violated, because this boy did exactly six problems, each of which was solved by at most two girls.
This is the “absurdity”, or “contradiction”, that we were seeking. Therefore there is a problem which is neither male nor female, and so was solved by at least three boys and at least three girls.
Solution – Problem # 2
Let $n$ be a positive integer. Consider an $n\times n$ chessboard consisting of $n^2$ unit squares.
A configuration of $n$ rooks on this board is peaceful if every row and every column contains exactly one rook. Find the greatest positive integer $k$ such that, for each peaceful configuration of $n$ rooks, there is a $k\times k$ square which does not contain a rook on any of its $k^2$ unit squares.
Answer: $\lfloor\sqrt{n-1}\rfloor$ (the brackets refer to the floor function, that is, the integer part of $\sqrt{n-1}$)
Solution: Let $m$ be a positive integer. We will show that (i) if $n > m^2$ then each peaceful configuration contains an empty $m\times m$ square, but (ii) if $n \leq m^2$ then there exists a peaceful configuration not containing such a square. These two statements together yield the answer.
(i) Assume that $n > m^2$. Consider any peaceful configuration. There exists a row $R$ containing a rook in its leftmost square. Take $m$ consecutive rows with $R$ being one of them. Their union $U$ contains exactly $m$ rooks. Now remove the $n – m^2 \geq 1$ leftmost columns from $U$ (thus at least one rook is also removed). The remaining part is an $m\times m^2$ rectangle, so it can be split into $m$ squares of size $m\times m$, and this part contains at most $m-1$ rooks. Thus one of those squares is empty.
(ii) Now we assume that $n \leq m^2$. Firstly, we will construct a peaceful configuration with no empty $m\times m$ square for the case $n = m^2$. After that we will modify it to work for smaller values of $n$.
Let us enumerate the rows from top to bottom as well as the columns from left to right by the numbers $0, 1, … , m² – 1$. Every square will be denoted, as usual, by the pair (r,c) of its row and column numbers. Now we put the rooks on all squares of the form $(im + j, jm + i)$ with $i,j = 0,1, … , m – 1$ (the picture below represents this arrangement for $m = 3$). Since each number from 0 to $m^2 – 1$ has a unique representation of the form $im + j (0 \leq i,j \leq m – 1)$, each row and each column contains exactly one rook.
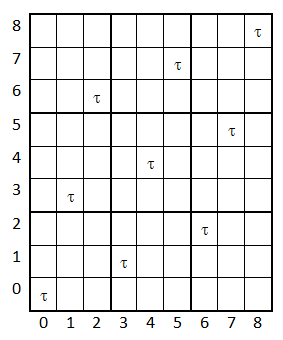
Next, we show that each $m\times m$ square $A$ on the board contains a rook. Consider such a square $A$, and consider $m$ consecutive rows the union of which contains $A$. Let the lowest of these rows have number $pm+q$ with $0 \leq p, q \leq m – 1$ (notice that $pm+q \leq m^2 – m$). Then the rooks in this union are placed in the columns with numbers
$$qm+p, (q + 1) m+p, … , (m – 1) m+p, p+1, m+(p+1), … , (q – 1) m+p+1$$
or, putting these numbers in increasing order,
$$p+1, m+(p + 1),…,(q – 1) m+p+1, qm+p, (q + 1) m+p, … , (m – 1) m+p.$$
One readily checks that the first number in this list is at most $m – 1$ (if $p = m – 1$, then $q = 0$, and the first listed number is $qm+p = m – 1$), the last one is at least $(m – 1)m$ and the difference between any two consecutive numbers is at most $m$. Thus one of the $m$ consecutive columns intersecting $A$ contains a number listed above, and the rook in this column is inside $A$, as required. The construction for $n = m^2$ is established.
It remains to construct a happy configuration of rooks not containing an empty $m\times m$ square for $n \leq m^2$. In order to achieve this, take the construction for an $m^2\times m^2$ described above and remove the $m^2 – n$ bottom rows together with the $m^2 – n$ rightmost columns. We will have a rook arrangement with no empty $m\times m$ square, but several rows or columns may happen to be empty. Clearly the number of empty rows is equal to the number of empty columns, so one can find a bijection (a one to one mapping) between them, and put a rook on any crossing of an empty row and an empty column corresponding to each other.







